Basics of Bayesian Statistics
Quick Notes
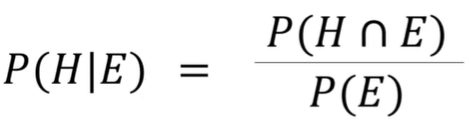
Hypothesis = H
Evidence = E
Three ways of saying the same thing. “Not E”
E prime == E’
E complement == Ec
Not E == ¬E
Example Problem 1:
Bob and Jane are sometimes late for work. 70% of the time neither of them are late. Bob is late 20% of the time, while Jane is late 25% of the time.
Last Monday Jane was late. Find the probability that Bob was late.
Evidence: Jane is late
Hypothesis: Bob is late
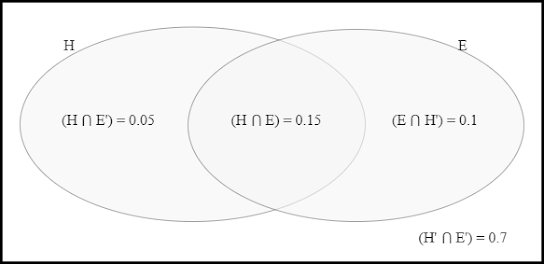
P(E' ⋂ H') = 0.7 => (70% of the time neither of them are late)
P(H) = 0.2 => (Bob is late 20% of the time)
P(E) = 0.25 => (Jane is late 25% of the time)
Step 1: Find out how much of the total both H and (E' ⋂ H')
0.2 + 0.7 = 0.9
Step 2: How much of E that is not part of H is there?
1 - 0.9 = 0.1
i.e. (E ⋂ H') = 0.1
Step 3: find what part of E intersects with H
0.25 - 0.1 = 0.15
Step 4: find (E' ⋂ H)
0.2 - 0.15 = 0.05
Step 5: find the probability that Bob is late given the evidence that Jane is late
Formula: P(H ⋂ E) / P(E)
0.15 / 0.25 = 3 / 5 = 60%
We now know that Bob has a 60% chance of being late when Jane is late. When Jane is not late he has a 20% chance of being late.
Here is a Venn Diagram to help visualize
Example Problem 2:
Bob loves to play Tennis, but especially when the weather is good. When it is sunny, the probability that he plays tennis is 80%. When it is not sunny, the probability is just 35%. There is a 60% chance that it is sunny on any given day. Last Saturday he played tennis. What is the probability that it was sunny last Saturday?
H: It was sunny last Saturday.
E: Bob played tennis last Saturday.
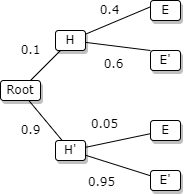
Create a tree with all possibilities and their complement percentages.

Probability that it was sunny and Bob played tennis can be seen by following the right side of
the tree: P(H ⋂ E) = 0.6 X 0.8 = 0.48
To calculate E by itself without H we can say:
Either it was sunny and Bob played tennis (H ⋂ E)
Or it may not have been sunny and Bob played tennis (H’ ⋂ E).
We then add these two things together (H ⋂ E) + (H’ ⋂ E)
(H ⋂ E) = 0.6 X 0.8 = 0.48
(H’ ⋂ E) = 0.4 X 0.35 = 0.14
P(E) = 0.48 + 0.14 = 0.62
apply Bayes theorem to get: H = 0.48/0.62 = ~77%
We now know it is 77% likely that It was sunny last Saturday
Example Problem 3:
During recessions there is a 40% chance that Bob will lose his job. Otherwise, there is a 5% chance.
In any given year there is a 10% chance of a recession.
Last year Bob lost his job. Find the probability that there was a recession.
E = Last year Bob lost his job
H = There was a recession
Build a tree with all possibilities.
Find the probability that he lost his job and there is a recession (H ⋂ E)

The probability of E is either there was a recession and he lost his job (H ⋂ E) Or there was not a recession and he lost his job (H’ ⋂ E)
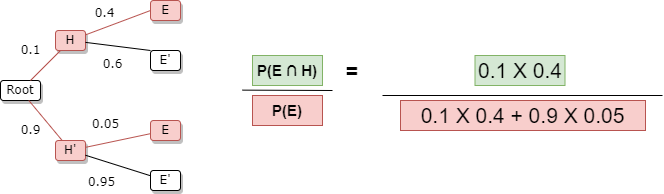
= ~47%